Chapter 1.4 Applications of Quadratic Equations

Pindling College Algebra   by Example  Series

Key Concept: Learn how to translate word problems that are quadratic in nature and use properties and operations
of the quadratic equation to solve such problems (see 1_3).

Skills to Learn:

1. Recognized quadratic problems as those with a variable to the second power.

2. Solve using factoring, complete the squares and the quadratic equation.

4. Check that answers are consistent with problem statement(s).

Example 1 - The length of a rectangle is 5 feet longer than that of its width. If its area is 36 feet, find its perimeter.

Understand the problem: Let the unknown width be x, then the length is x + 5. Since the area of a rectangle is the length times the width, (note 36 is given as the area above). Strategy: If we solve for x we get the width and so can find the length (x + 5) and then the perimeter (x + (x + 5) Finding x is solving a quadratic equation:

Standard form: already in standard form: So: becomes: Quadratic Equation: So the root, x = So and Only x = 4 is an appropriate solution of this problem.	Zero Form (Factor) So (x + 9 ) = 0, x = -9 and (x - 4) = 0, so x = 4 Since this represents a width which must be positive, only 4 is an appropriate solution.
Completing the Square (next group x terms) (complete the square) (Vertex Form ) Vertex is (2.5, -42.25) Now can solve for x , So , So x = - 9 and 4	Graphical Solution - Graph the function and find x when A = 0 (x-axis)

Check Solution: If x = 4 then length is 4 + 5 = 9 and Area = 4 x 9 = 36 (This checks) So perimeter is 2(width) + 2(length) = 2(4) + 2(9) = 8 + 18 = 26 feet

Example 2 - A family trip from New York to Michigan is about 800 miles. If a family on its return trip increased the
average speed by 20 miles and saves 3 hours of driving time. What was the average speed in each direction?.

Understand the problem: Since the time coming back minus the time going is 3 hours, we can write relationships for these times. Remember that time and speed are related by this formula: So since the distance traveled in either directions is 800 miles, : , where s is the speed going from NY to MI. So time going minus time coming back is: , solve for speed by finding s.

Standard form: not in standard form: : , or Divide by 2:	Zero Form (Factor) : Not an integer solution for factoring Quadratic Equation: So the root, s = So and Only s = 63.7111 mph is an appropriate solution of this problem. So s+20 = 83.7111 mph (must be in a hurry since violated the maximum speed limit of 70 mph)
Completing the Square : next group x terms) (complete the square) (Vertex Form ) Vertex is (-10, -16300) Now can solve for s , So , So x = - 93.711 and 63.71	Graphical Solution - Graph the function : and find x when t = 0 (x-axis), so s = 63.7111 mph

Check Solution: If s =63.7111 then (This checks) So speed going to MI was 63.71 mph and return speed was 83.71 mph

Example 3 - Vertical Motion Problem. A ball is thrown into the air and its height, h above the ground in feet with
respect to time in seconds is given by the equation 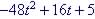. When will the ball hit the ground?

Understand the problem: Formula given is quadratic: . So if it is a function of height, H with respect to time, t, then The ball will hit the ground when H = 0, So find t when H = 0 or solve for

Standard form: already in standard form: Where a = -48, b = 16 and c = 5 Quadratic Equation: So the root, x = So and Only t = 0.5299 sec is an appropriate solution of this problem.	Zero Form (Factor) : Not an integer solution for factoring
Completing the Square : next group x terms) (complete the square) (Vertex Form ) Vertex is Now can solve for t , So , So t = - 0.1966 and 0.5299	Graphical Solution - Graph the function : and find t when h = 0 (x-axis), so t = 0.53 second

Check Solution: If t =0.5299 then: (This checks) So the ball hits the ground 0.53 second after it is thrown.