|
General Statistics
|
Examples
Normal Probability Distribution
|
Normal
/ Continuous Probability Program
Normal (z-score
Reference Table) Binomial
Distribution
Question 1 Scores on a class exam have a mean of 85% and a standard
deviation of 5%.
Let x represents students test result on the exam (assume x is a random
normal variable).
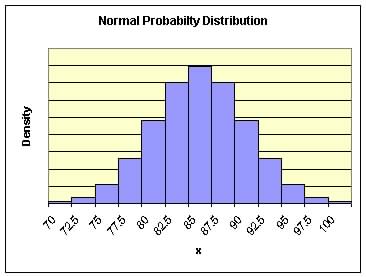
(1) Draw a probability distribution of the student results
(2) What is the probability that a randomly selected student will get
a grade of:
(a) Higher than 95% or less than 75%?
(b) Higher than the 85%?
(c) Between 90 and 95%?
(d) Lower than 90%?
(e) Between 75 and 85%?
(f) Within one standard deviation of the mean?
(g) Within two standard deviations of the man?
Solutions
(1) Probability Distribution of Exam Results:
mean = 85 and standard deviation = 5
 |
(a) Pr[>95 or
<75] = Pr[>95] + Pr[<75] = 0.02275 - (1-0.97725) =
Pr[>95 or <75] = 0.02275 + 0.02275 = 0.0455
(b) Pr[>85] = 1 - Cum Pr[85] = 1 - ½ = ½
(c) Pr[90<x<95] = 0.97725 - 0.841345 = 0.1359
(d) Pr[<90] = Cum Pr[90] = 0.8413
(e) Pr[75<x<85] = 0.5 - 0.02275 = 0.4773
(f) Within 1 std of mean:
Pr[80 to 90] = 0.841345 - 0.158655 = 0.6827
(g) Within 2 stds of mean:
Pr[75 to 95] = 0.97725-0.02275 = 0.9545 |
| Probability Calculation from program
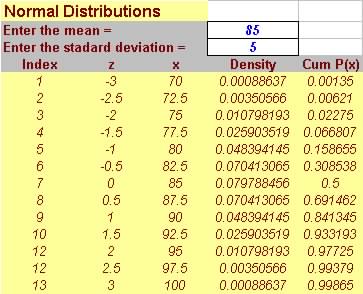
|
Question 2 Suppose z represents the Standard normal variable.
If a value is selected at random from the
z - distribution, find the probability that z is:
(a) less than 0
(b) Between -0.67 and 0.
(c) Between -2.3 and -1.45.
(d) Between -0.73 and 2.31.
(e) Less than 1.96
(g) Within one standard deviation of the mean
Solutions
From Standard Normal Table -
(a) Pr[<0] = Cum Pr[0] = 0.5
(b) Pr[-0.67 to 0] = Pr[0] - Pr[-0.67] = 0.5 - 0.2514
= 0.2486
(c) Pr[-2.3 to -1.43] = Pr[-1.43] - Pr[-2.3] = 0.0764
- 0.0107 = 0.0655
(d) Pr[-0.73 to 2.31] = Pr[2.31] - Pr[-0.73] = 0.9896
- 0.2327 = 0.7569
(e) Pr[< 1.96] = Cum Pr[1.96] = 0.9750
(g) Pr[-1 to 1] = Pr[1] - Pr[-1] = 0.8413 - 0.1587
= 0.6826
Question 3 (6.21) A computer chip component is designed so that
they are replaced after 5 years.
A historical study of 10,000 parts over a 10 years period shows that
the mean time before first repair is
36 months and the standard deviation is 7 months.
(a) If the company plans to guarantee the chip component for 2 years,
what percent of the chip component will not satisfy the guarantee?
(b) The company plans to only repair 5% of all components, what should
the guarantee period be?
Solutions
(a) So for 2 years or 24 months, z-score = (24 - 36) / 7 = -1.7143..,
Guarantee not covered is
Cum Pr[z = -1.7143] = 0.0436 or 4.36%
(b) 5% repair equals a probability of 0.05 which correspond to z-score
= -2.33
So z=-2.33 = (x - 48)/7, x = (7 x -2.33) + 48 = 31.69
months.
Question 4. (6.29) Assume that an experiment is a binomial experiment:
(a) Use the binomial table or probability distribution to find the probability
of x between 5 and 7, inclusive
where x is the number of defect, n = 15 trials and p = 0.6.
(b) Given the information in part (a) use the normal approximation to
the binomial to find x between 5 and 7 inclusive.
Solutions
| Binomial Pr[5 + 6 + 7 ] =
0.2038

|
Normal Approx. Pr[5 + 6 +
7] = 0.2038
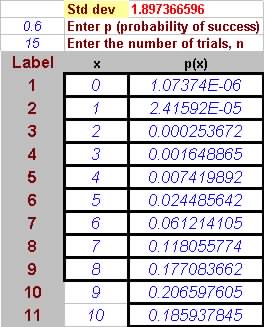 |
Question 5 (6.41) A normal population has mean of 600 and standard
deviation of 300.
If the sample size is n= 100.
(a) Find the sample mean
(b) Find the sample standard deviation
(c) Find Pr[585 < x < 615]
(d) Find Pr[x > 600]
(e) If one value of x is selected, find Pr[585 < x < 615], compared
with part (c)
(f) If one value of x is selected, find Pr[x > 600]
Solutions
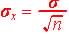
(a) Sample mean is same of population mean = 600
(b) Sample standard deviation is 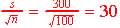 (10)
(10)
(c) Pr[585 < x < 615], compute z-score (585-600)/30 = -0.5 etc.
So
Pr[-0.5 < z < 0.5] = 0.6915 - 0.3085 = 0.3830
(d) Find Pr[x>630] , find z-score 530 - 500 / 30 = 1. Pr[ ] =
1 - 0.8413 = 0.1587
(e) If one value of x is selected, find Pr[585 < x < 615], compared
with part (c)
Question 6. (6.57) let x be a normal random variable with mean
18 and standard deviation of 2. Find the following:
(a) The 10th percentile
(b) the 95th percentile
(c) The percent rank of x = 19
(d) The percent rank of x = 14.
Solutions
(a) The 10th percentile is z.010 = (x - mean) / std: z of
0.10 = -2.32 (where Pr = 0.10), mean = 18 and std = 2
So x = (-2.32 x 2) + 18 = 13.36
(b) The 95 Th. percentile (z = 1.65 when Pr = 0.95), x = (1.65 x 2)
+ 18 = 21.3
(c) The percent rank of x = 19: z = (19 - 18) / 2 = 0.5, Pr[z=0.5]
= 0.6915 or 69.15%
(d) The percent rank of x = 14 : z = (14 - 18) / 2 = -2, Pr[z=-2] =
0.02275 or 2.28 %




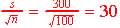 (10)
(10)