In this text we will explore problems when two or more functions intersect with each other.

The simplest form is the intersection of two linear functions or the intersection of a linear function with a quadratic function. Often its is necessary to determine the points where the graphs of both function intersects or crosses each other.

In some cases finding the point(s) where two functions intersect can be an algebraic solution and in other cases one must use a graphical method to find the solution(s).

Example 3. Find the point where the these two functions intersect: y = 3x -2 and y = -2x + 8

Finding Point(s) of Intersections of Functions - Algebraic Approach

To find the point(s) where two functions intersect first set the functions equal to each other and solve for x and then substitute x into any of the equation and solve for y. There are other ways of doing this algebraically, can you think of another?

So set y = 3x - 2 = -2x + 8

3x -2 = -2x + 8

Group like terms: 3x + 2x = 8 + 2 = 5x = 10 or x = 2

Substitute x = 2 into y = 3x - 2 = 3(2) - 2 = 6 - 2 = 4

So point of intersection is (x, y) = (2, 4)

Finding Point(s) of Intersections of Functions - Graphical Approach

If you plot both functions on the same axis and use the [ISECT] function to find the point of intersection, 
then you have found a graphical solution to the problem:

The [ISECT] function is found under the [Graph] Menu and will be demonstrated in class.

Therefore a graphical solution to the problem in Example 3 is:

Figure 2.8 Graphical Solution to Simultaneous Linear Functions: 
y = 3x -2 and y = -2x + 8
 

Example 4. Find the points where the following two functions intersect:  and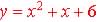 

Table 2.4 Intersection of two Curves: Algebraic and Graphical Solutions

Algebraic Solution: Set equation equal to each other: Move all to right: 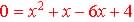 So when y = 0, x = 1 and 4 From y = 6x +2, when x = 1 and 4 we have: (1, 8) and (4, 26)

Graphical Solution: Figure 2.9
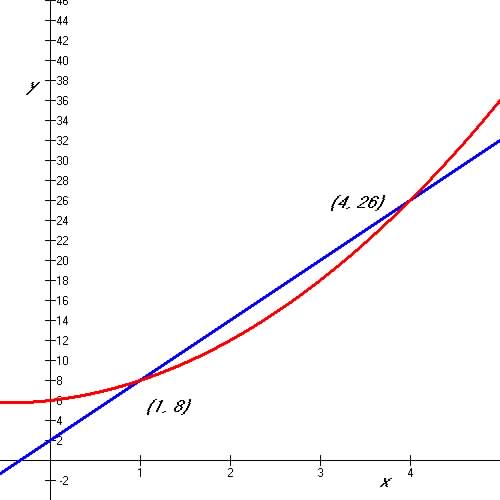