Analysis of Variance (ANOVA) is a statistical test used to determine if more than two population means are equal.
The test uses the F-distribution (probability distribution) function and information about the variances of each population (within)
and grouping of populations (between) to help decide if variability between and within each populations are significantly different.

So the method of ANOVA test the hypotheses that:
 

H0:  or  Ha: Not all the means are equal

1. Know the purpose of the analysis of variance test.

The analysis of variance (ANOVA) test statistics is used to test if more than 2 population means are equal.

2. Know the difference between the within-sample estimate of the variance and the between-sample estimate of the variance
and how to calculate them.

When comparing two or more populations there are several ways to estimate the variance.

The within-sample or treatment variance or variation is the average of the all the variances for each population and is an estimate of
whether the null hypothesis, H₀ is true or not.

, for j = 1 to k, where k is the number of samples or populations.

Example: Given 5 populations with sample variances: 2.0, 2.2, 2.35, 2.41 and 2.45, the within standard deviation is:

The within-sample variance is often called the unexplained variation.

The between-sample variance or error is the average of the square variations of each population mean from the mean
or all the data (Grand Mean, ) and is a estimate of  only if the null hypothesis, H₀ is true.
When the null hypothesis is false this variance is relatively large and by comparing it with the within-sample variance
we can tell statistically whether H₀ is true or not.

The between-sample variance is associated with the explained variation of our experiment.

Example: Given the means of 5 samples: 210, 212, 213, 214 and 214,

Then another estimate of the sample variance of the means is:

for j = 1 to k, where k is the number of samples or populations.
 

Sample	Sample mean  (1) ()	Mean - Grand Mean (2) ()	Sum of Square  ()2 (3)
1	210	1	6.76
2	212	2	0.36
3	213	3	0.16
4	214	4	1.96
5	214	5	1.96
	Average (1) =212.6		Total (3) =11.2

Grand Mean,  = 212.6, k = 5, and s²_B (between) = ()² / (k-1) = 11.2 / 4 = 2.8

When the null hypothesis, H₀ is true the within-sample variance and the between-sample variance will be about the same;
however, if the between-sample variance is much larger than the within, we would reject H₀.

If the data from both examples above are from the same 5 samples or populations then a ratio of both estimates of the variance
would give the following:

This ratio has a F-distribution.

3. Know the properties of an F Distribution.

There is an infinite number of F-Distribution based on the combination of alpha significance level,
the degree of freedom (df₁) of the within-sample variance and the degree of freedom (df₁) of the between-sample variance.

The F-Distribution is the ratio of the between-sample estimate of  and the within-sample estimate:

If there are k number of population and n number of data values of the all the sample,
then the degree of freedom of the within-sample variance, df₁ = k -1 and
the degrees of freedom of the between-sample variance is given has df₂ = n - k.

The graph of an F probability distribution starts a 0 and extends indefinitely to the right.
It is skewed to the right similar to the graph shown below.
 

F-Distribution Graphs:

4. Know how sum of squares relate to Analysis of Variance.

Remember back in Chapter 3 (Regression) we introduced the concept that the total sum of squares
is equal to the sum of the explained and unexplained variation; this section is an extension of that discussion.
 

Total Variation = Explained Variation + Unexplained Variation.

Sum of Squares

The sum of squares for the between-sample variation is either given by the symbol SSB (sum of squares between)
or SSTR (sum of squares for treatments) and is the explained variation.

To calculate SSB or SSTR, we sum the squared deviations of the sample treatment means from the grand mean
and multiply by the number of observations for each sample.

The sum of squares for the within-samplevariation is either given by the symbol SSW (sum of square within)
or SSE (sum of square for error).

To calculate the SSW we first obtained the sum of squares for each sample and then sum them.

The Total Sum of Squares, SSTO = SSB + SSW

The between-sample variance, , where k is the number of samples or treatment and is often
called the Mean Square Between, ,

The within-sample variance, , where n is the total number of observations in all the samples is often
called the Mean Square Within or Mean Square Error, ,

Examples Compute the SSB, SSE and SSTO for the following samples:
 

Rows, i	Treatment of samples j ( 1 to k), k = 3
	Sample 1	Sample 2	Sample 3
1	77	83	80
2	79	91	82
3	87	94	86
4	85	88	85
5	78	85	80
Mean	81.2	88.2	82.6
Grand Mean,	84

Sum of Square Worksheet
 

Rows, i	Treatment of samples j ( 1 to k), k = 3
	SS (Column 1)	SS (Column 2)	SS (Column 3)
1	(77-81.2)2 = 17.64	(83-88.2)2 = 27.04	(80-82.6)2 = 6.76
2	(79-81.2)2 = 4.84	(91-88.2)2 = 7.84	(82-82.6)2 = 0.36
3	(87-81.2)2 = 33.64	(94-88.2)2 = 33.64	(86-82.6)2 = 11.56
4	(85-81.2)2 = 14.44	(88-88.2)2 = 0.04	(85-82.6)2 = 5.76
5	(78-81.2)2 = 10.24	(85-88.2)2 = 10.24	(80-82.6)2 = 6.76
SSj (Col)	80.8	78.8	31.2
Sample size, nj	5	5	5

SSW = SSE =  = 80.8 + 78.8 + 31.2 = 190.8

SSB = SSTR =  = 5[(81.2 - 84)² + (88.2 - 84)² + (82.6 - 84)² ] =137.2

MSB =  and MSW = MSE = 

F = 

5. Know how to construct an ANOVA Table.

The various statistics computed from the analysis of variance above can be summarized in an ANOVA Table
as shown below: These summaries are then used to draw inference about the various samples or treatments of which we are studying.

ANOVA Table - Basic layout:
 

Source	Sum of Squares (SS)	Degree of Freedom  (df)	Mean Square	F-Statistics	P-value
Between Samples (Explained)	SSB	k-1	MSB=	F=	Value from Table
Within  Samples (Unexplained)	SSE	n-k	MSE=
Total	SSTO	n-1

The ANOVA table is easily constructed from the ANOVA program by entering each observations for each sample in
appropriate columns and deleting any division by 0 in selected regions of the program.

For the data above the ANOVA table is:
 

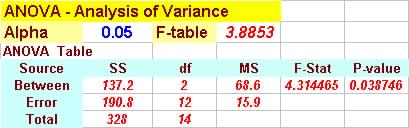6. Know how to interpret the data in the ANOVA table against the null hypothesis.

The ANOVA table program computes the necessary statistics for evaluating the null hypothesis that
the means are equal: H₀: .

Use the degrees of freedom and an alpha significance level to obtain the expected F-Distribution statistics
from the lookup table or from the ANOVA program.

Acceptance Criteria for the Null Hypothesis:

If the F-statistics computed in the ANOVA table is less than the F-table statistics or
the P-value if greater than the alpha level of significance, then there is not reason to reject the null hypothesis
that all the means are the same:
 

That is accept H0 if: F-Statistics < F-table or P-value > alpha.

For the example above we would reject the null hypothesis at the 5% significance level and conclude
that the means are not equal since F-Stat > F-Table.

7. Know the procedure for testing the null hypothesis that the mean for more than two populations are equal.

Step 1 - Formulate Hypotheses:

H₀:  and

H_a: Not all the means are equal

Step 2. Select the F-Statistics Test for equality of more than two means

Step 3. Obtain or decide on a significance level for alpha, say 

Step 4. Compute the test statistics from the ANOVA table.

Step 5. Identify the critical Region: The region of rejection of H₀ is obtained from the F-table with alpha and degrees of freedom (k-1, n-k).

Step 6. Make a decision:

That is accept H₀ if: F-Statistics < F-table or P-value > alpha.

Worksheet for Computing Analysis of Variance Statistics:
 

Rows, i	Treatment of samples j ( 1 to k
	Sum of Square j=1	Sum of Square j=2	Sum of Square j=3	Sum of Square j=4	Sum of Square j=5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
SSj (Column Total)
Sample size, nj
SSW = SSE = =
SSB = SSTR =  =

ANOVA Table
 

Source	Sum of Squares (SS)	Degree of Freedom  (df)	Mean Square	F-Statistics	P-value / F-Table
Between Samples (Explained)	SSB=	k-1=	MSB==	F==
Within  Samples (Unexplained)	SSE=	n-k=	MSE==
Total	SSTO=	n-1=